책에서 제시하는 몇 가지 수학 개념들이 있다.
Vector, Matrix, Transform이 있는데 학교에서 흔히 접하는 내용들이기는 하나,
용어적인 부분에서 낯설 수 있다.
때문에 여기서는 매우매우 기초적인 개념을 제외한 부분들을 용어 설명 위주로 풀어나가고자 한다.
Coordinate System(좌표계)

Left-handed Coordinate System(왼손 좌표계) - 왼손 엄지, 검지, 중지 손가락이 서로 수직이 되도록 폈을 때,
엄지 손가락이 X축, 검지 손가락이 Y축, 중지 손가락이 Z축을 가르킨다.
Right-Handed Coordinate System(오른손 좌표계) - 왼손 엄지, 검지, 중지 손가락이 서로 수직이 되도록 폈을 때,
엄지 손가락이 X축, 검지 손가락이 Y축, 중지 손가락이 Z축을 가르킨다.
Unit Vector(단위 벡터) - 주어진 Vector를 크기(Magnitude)를 1로 맞춘 Vector.
Vector의 순수한 방향을 나타내는 용도로 사용된다.
반대로 Vector u의 크기를 나타낼 때는 ||u||라고 표시한다.
Normalization(정규화) - Vector를 Unit Vector로 만드는 작업.
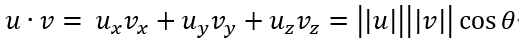
Dot Product(= Inner Product, Scalar Product)(내적) - 동일한 차원에 존재하는 두 Vector의 성분들을 곱한 뒤 합산.
Dot Product 한 값은 두 Vector의 크기와 그 사이 각의 cos 값의 곱과 동일하다.
때문에 사이각을 구하는 데에 매우 유용하게 사용된다.

Orthogonal Projection(직교투영, 정사영) - 어떤 Vector에서 특정 Vector 성분을 분리하는 작업.
위 식에서, P는 Vector V에 대해 Vector n 성분. 즉, n과 같은 방향(Direction)을 가진 Vector를 나타낸 것이다.
이와 같이 Vector V에 대해서 Vector n에 대한 성분인 Vector P를 구하는 것을 Orthogonal Proejction이라 한다.
V에서 P를 뺀 나머지. 즉 P와 수직인 V의 성분은 Prep(Perpendicular[수직의])으로 표현한다.
Orthonomal(직교의) - 주어진 Vector들이 서로 수직인 상태를 가르킨다.
Orthonomal group(정규집교 집합) - 어떤 Vector group에 속한 모든 Vector들이 서로 Orthonomal한 상태.
흔히 볼 수 있는 Orthonomal group은 어떤 Vector를 X, Y, Z축에 대해 Orthogonal Projection 한 결과들의 집합이다.
Orthogonalization(직교화) - Orthonomal 하지 않은 Vector group을 Orthonomal group으로 만드는 과정.

Gram-Schmidt Orthogonalization(그람-슈미트 직교화) - n개의 Vector group을 Orthogonalization 하는 방법

Cross Product(=Outer Product)(외적) - 두 Vector에 대해서 모두 직교인 Vector를 구하는 작업.
이 연산은 두 개의 축을 알고 있을 때 나머지 하나의 축을 구하는데 매우 유용하다.
Cross Product는 연산한 Vector 순서에 따라 적용되는 Coordinate System의 방향을 따라 간다.
즉, Left-Handed라면 Cross Product 결과도 Left-Handed, Right-Handed라면 Product 결과 역시 Right-Handed이다.
2차원에서는 Cross Product가 존재하지 않는다.
하지만 유사 외적을 통해 어떤 Vector에 대한 수직 Vector를 구할 수는 있다.
Position Vector(위치 벡터) - 3차원 공간 안의 한 위치를 나타내는 Vector.
본 책에서는 Dot(점)과 Position Vector(위치 벡터)를 같은 의미로 사용한다.
Dot을 Position Vector로 사용했을 때 한 가지 부차적인 효과를 얻는다.
바로 Dot에 대해서는 의미가 없는 Vector 연산이 가능하다는 점이다.
예를 들어, p(dot) + v(vector) = q(vector)는 p+v라는 vector를 q로 표현한 것이기도 하지만,
p를 v만큼 옮겼을 때의 점의 위치 q이기도 하다.
'내용정리 > DirectX12' 카테고리의 다른 글
| 05. DirectXMath.h에서의 Vector 관련 기능 (0) | 2020.05.22 |
|---|---|
| 04. 기초 필수 수학 - Transform (0) | 2020.05.22 |
| 03. 기초 필수 수학 - Matrix (0) | 2020.05.15 |
| 01. DirectX 12 Project Setting (0) | 2020.05.08 |
| 00. 글쓰기에 앞서 (0) | 2020.05.08 |