Linear Transform(선형 변환)
어떤 Vector에 대한 함수 중 다음 조건을 만족하고, 오직 그럴 때, 그 함수를 Linear Transform이라 부른다.

Linear Transform일 때에는 다음 또한 만족한다.

Standard Basis Vector(표준기저벡터)
현재 Coordinate System의 Axis들과 같은 방향인 Unit Vector.
Standard Basis Vector를 이용하면 일반 Vector도 다음과 같이 나타낼 수 있다.

이를 Linear Transform하면 그 Linearity가 성립하여 다음이 성립한다.

이는 이전에 한번 언급했던 Linear Combination이다.
따라서 하나의 Vector와 Matrix의 곱셈으로 표기할 수 있다.

이러한 Matrix A를 Linear Transform τ의 Matrix Expression이라 부른다.
Scaling(비례)
물체의 크기를 바꾸는 효과를 내며, 선형변환이다.
Scaling Transform은 다음과 같이 정의된다.

Matrix Expression은 다음과 같다.

이 Matrix를 Scaling Matrix 라고 부른다.
Rotation(회전)
Vector v를 Axis n에 대해서 Θ 각도만큼 회전시키는 Transform이 있다.
이에 대한 Matrix Expression은 다음과 같다.

Rotation Matrix에는 흥미로운 속성이 있다.
Rotation Matrix의 각 Row Vector는 Unit size이고, Row Vector들은 서로 Orthogonal하다.
따라서 Rotation Matrix는 Orthogonal Matrix이다.
Orthogonal Matrix는 Inverse Matrix이 자신의 Transposed Matrix와 같다는 속성이 있다.
이로 인해 Rotation Matrix의 Inverse Matrix는 다음과 같이 정의될 수 있다.

일반적으로 Inverse Matrix을 쉽고 효율적으로 계산할 수 있는 Orthogonal Matrix를 다루는 것이 바람직하다.
특히 Rotation Axis가 Standard Basis Vector인 경우에는 Rotation Matrix가 매우 간단해진다.
다음은 차례대로 x축, y축, z축에 대한 Rotation Matrix이다.

Homogeneous Coordinate(동차좌표)
3차원 Vector에 w 성분을 추가한 4-Element의 형태를 나타낸다.
추가된 성분 w는 서술하는 것이 Dot인지 Vector인지에 따라 그 값이 달라진다.
Vector인 경우에는 w 값은 0이, Dot인 경우에는 1이 된다.
나중에 보면 알겠지만, Dot에 대해서 w = 1인 경우, 정확한 이동이 가능하다.
반대로 Vector에 대해서 w = 0인 경우, 이동 시 Vector가 변하지 않는다.
Rigid Body Transformation(강체 변환)
Transform 시 물체의 형태가 그대로 유지되는 Transformation.
Affine Transformation(아핀변환)
Linear Transformation에 Translation이 결합된 것.
Lintear Transformation으로 서술하지 못하는 Transformation을 서술하기 위해 사용된다.
이를 Matrix로 나타내면 아래와 같다.

여기에 w = 1인 HomogeneousCoordinate를 도입하면 아래와 같이 더 간결하게 표기할 수 있다.

위 식에서 사용된 4×4 Matrix를 Affine Transform의 Matrix Expression이라 부른다.
여기서 추가된 b는 하나의 Translation을 나타낸다는 점을 주목하자.
Vector에는 위치가 없으므로, 이 이동은 적용되지 말아야 한다.
하지만 Affine Transformation의 Linear Transformation 부분은 여전히 벡터에 적용되어야 한다.
Vector의 w = 0으로 설정함으로써, b에 의한 Translation은 적용되지 않는다.
그렇다면 Affine Transformation의 기하학적 의미는 무엇일까?
이는 Affine Transform을 Row Vector로 표시해보면 조금 더 쉽게 알아차릴 수 있다.

τ는 Rotation Transformation이므로 길이와 각도가 보존된다.
구체적으로, τ는 Standard Basis Vector i, j, k만 새로운 방향 τ(i), τ(j), τ(k)로회전한다.
Vector b는 단지 원점으로부터의 변위를 나타내는 Position Vector일 뿐이다.
이는 책상 위에 가지런히 올려져 있는 큐브를 손으로 집어 올린 모양을 생각하면 편하다.
또한 이런 원리는 Scaling이나 Skew(기울이기)에도 동일하게 적용된다.
그저 Standard Basis Vector가 왜곡되어 있을 뿐이다.
Identity Transformation(항등변환)
주어진 인수를 그대로 돌려주는 Linear Transformation.
이 Transformation의 Matrix Expression은 Unit Matrix이다.
이러한 맥락에서, Translation Transformation을 Affine Transformation으로 정의할 수 있다.
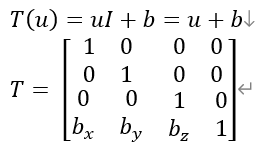
이를 Translation Matrix라고 부른다.
Change of Coordinate Transformation(좌표 변경 변환)
한 Coordinate System의 Coordinate를 다른 Coordinate System의 Coordinate로 Transform 하는 것을 말한다.
여기서 강조하고 싶은 것은 기하구조가 아니라 Coordinate System이 바뀐다는 점이다.
또한 Change of Coordinate Transformation은 결합 법칙이 성립된다.
이는 작게 보여도 생각보다 큰 성능 향상으로 이어지는 경우가 적지 않다.
Coordinate System F, G, H가 있다고 가정하자.
Change of Coordinate Transformation A는 Coordinate System F에서 G로, B는 G에서 H로 Transform 하는 Transformation이다.
이 때, C=AB일 때, C가 가지는 의미는 Coordinate System F에서 H로 Transform 하는 Transformation이다.
반대로 C의 Inverse Matrix는 Coordinate System H에서 F로 Transform 하는 Transformation이다.
마찬가지로 Inverse Matrix A와 B 역시 각각 G에서 F로, H에서 G로 Transform 하는 Transformation을 뜻한다.
여기서 다루는 Coordinate System은 모두 Reversible하다.
즉, 모든 Change of Coordinate Transformation Matrix는 Inverse Matrix가 존재한다.
또한 앞서 언급했던 모든 Rigid Body Transformation과 Change of Coordinate Transformation은 모두 동치이다.
생각해보면 당연하다. Change of Coordinate Transformation은 Coordinate System의 위치와 방향이 다 다르다.
때문에 한 Coordinate system에서 다른 Coordinate System으로의 Transformation에는 Coordinate들의 Rotation과 Translation이 필요하다.
이런 부분을 구해보면 결국 동일한 형태의 공식에 도달한다.
둘의 차이는 Transformation을 해석하는 방법의 차이 뿐이다.
----------------------------
이로써 책에서 언급한 이론적인 부분에 대한 정리는 모두 마쳤습니다.
다음에는 지난 2~3주간 설명한 부분들에 대한 DX12에서의 관련 함수들을 정리하고,
본격적인 DirectX12 Programming 입문과 함께 기본 코드의 분석을 병행하겠습니다.
'내용정리 > DirectX12' 카테고리의 다른 글
| 06. DirectXMath.h에서의 Matrix, Transformation 관련 기능 (0) | 2020.05.29 |
|---|---|
| 05. DirectXMath.h에서의 Vector 관련 기능 (0) | 2020.05.22 |
| 03. 기초 필수 수학 - Matrix (0) | 2020.05.15 |
| 02. 기초 필수 수학 - Vector (0) | 2020.05.08 |
| 01. DirectX 12 Project Setting (0) | 2020.05.08 |